Simulation of Kähler potentials

For a given probability density \(\sigma\), consider the vorticity-type equations

\[\dot\rho + \{\psi,\rho\}=0, \qquad \Delta \psi = \rho -\sigma\]

where $\rho$ is a probability density and $\psi$ is the stream function. We can discretize these equations via matrix hydrodynamics, which yields the isospectral matrix flow

\[\dot R = \frac{1}{\hbar}[P,R],\qquad \Delta_N P = R - F .\]

It is interesting to compare long-time simulations of such systems with the predictions from statistical mechanics (corresponding to optimal potentials in Kähler geometry).

We randomly generate three background measures \(R\) (via a spherical harmonics expansion with maximum wave-number \(\ell=3\)). Then we use random initial conditions (with maximum wave-number \(\ell=10\)) and run the simulations. The results are given below (to the left is the background measure \(R\)).

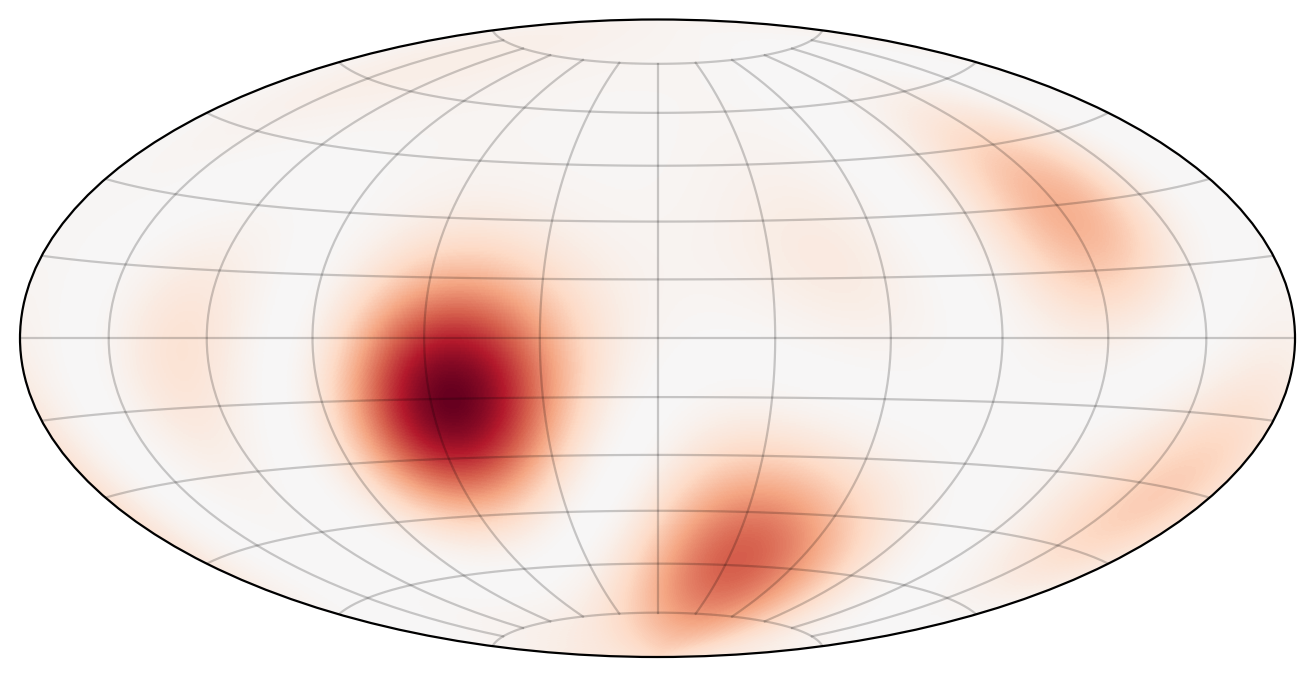
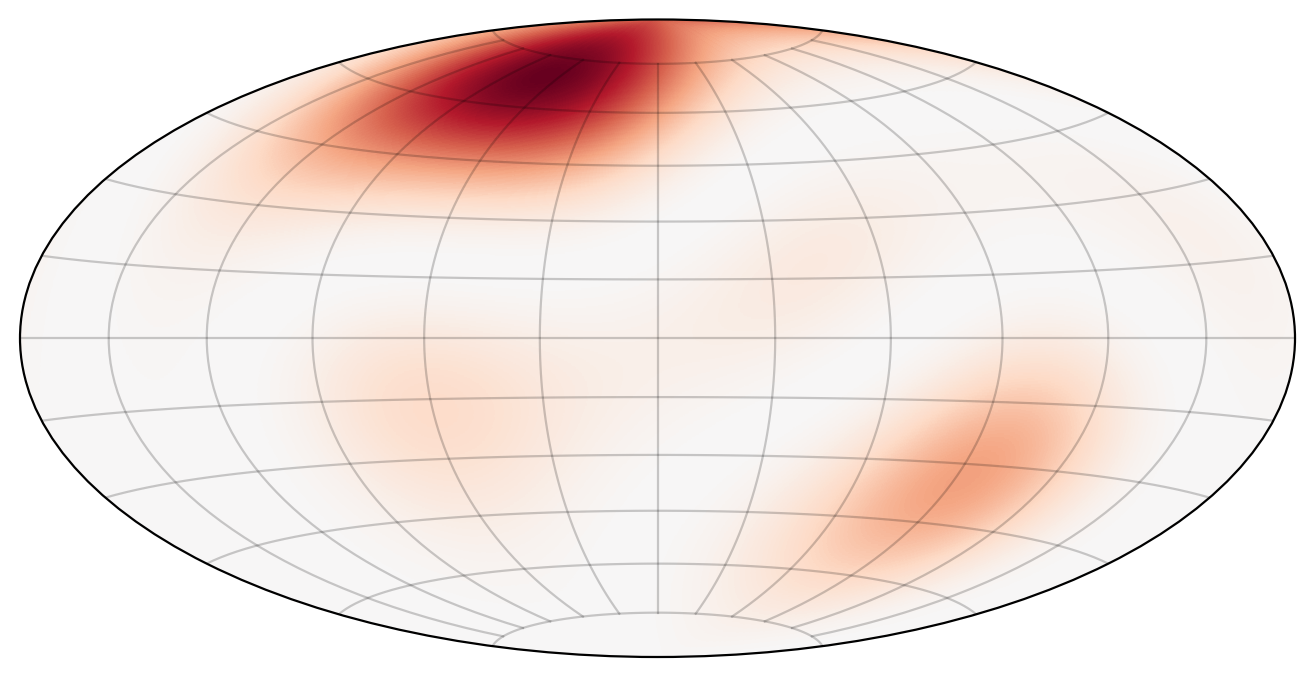
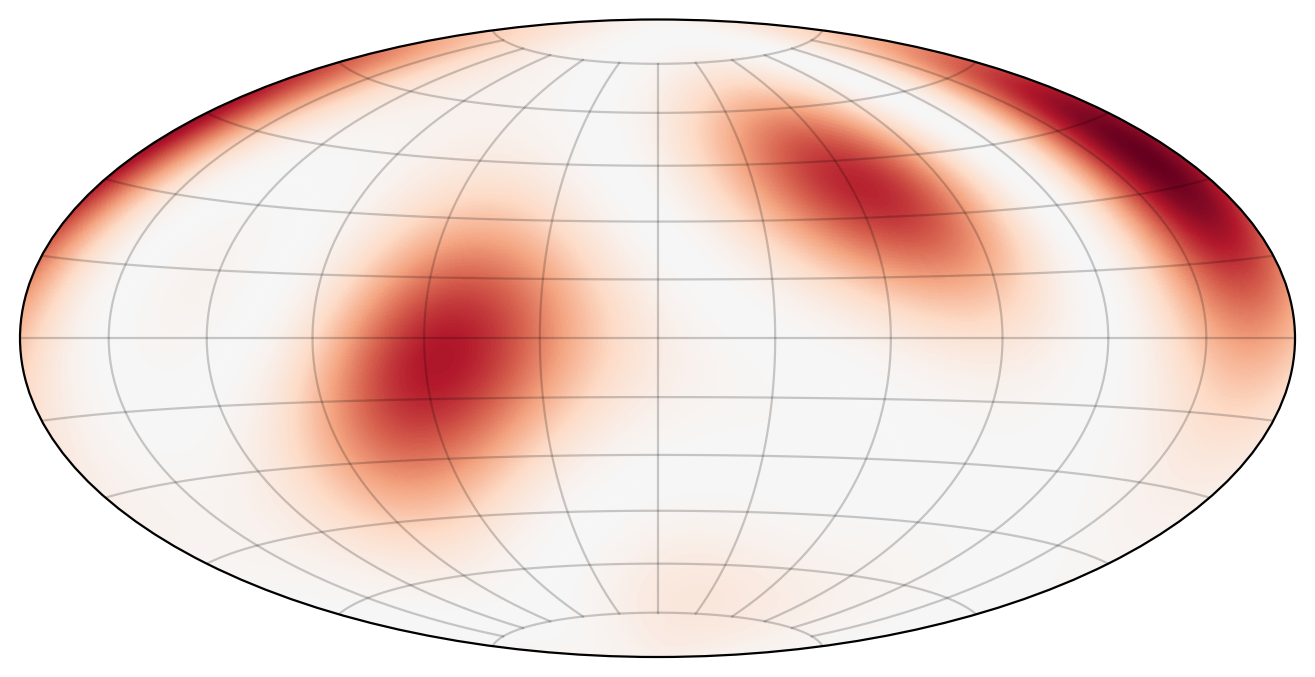
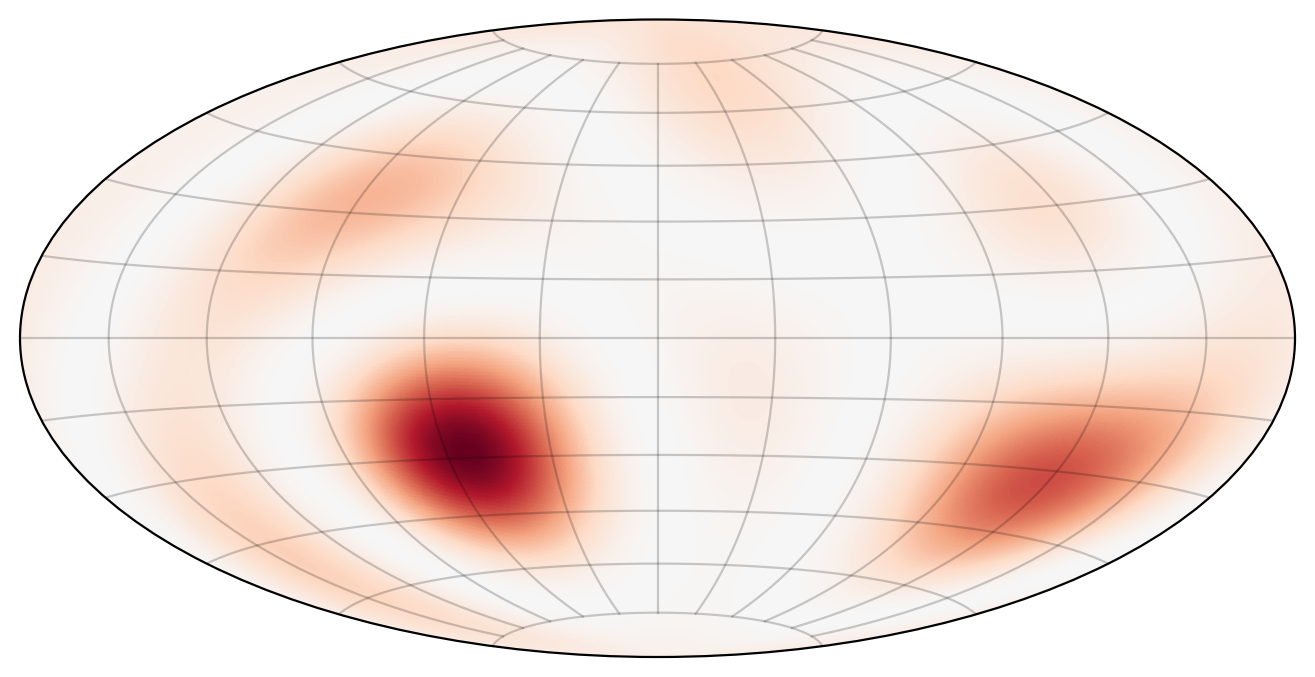
Observations:

• In most simulations, the mass gets concentrated around the strongest stationary blobs.

• In one simulation (a single blob found an “integrable-like” motion)