Magnetohydrodynamics with viscosity
The 2-D magnetohydrodynamic (MHD) equations can be formulated in terms of a fluid vorticity field \(\omega\) and a magnetic vorticity field \(\theta\)
\[\dot\omega = \{-\psi, \omega\} + \{-\beta, \theta\} +\nu \Delta\omega\] \[\dot\theta = \{-\psi, \theta\} \phantom{+ \{-\beta, \theta\} +\nu \Delta\omega}\]where \(\nu \geq 0\) is the viscosity (acting as a dissipative force on the fluid vorticity only), \(\psi = \Delta^{-1}\omega\) is the stream function, and \(\beta = \Delta\theta\) is the magnetic stream function. Geometrically, this is a Lie-Poisson system on a magnetic extension semi-direct product Lie algebra \(\mathfrak{g}\ltimes\mathfrak{g}^*\). The Hamiltonian for the system is given by
\[H(\omega,\theta) = \frac{1}{2}\int_{S^2} (\omega\Delta^{-1}\omega + \theta\Delta\theta)\mu .\]where \(\mu\) is the symplectic form (likewise the area-element) of the sphere \(S^2\). We can split the energy into two components, corresponding to the variables \(\omega\) and \(\theta\):
\[E_1(\omega) = \frac{1}{2}\int_{S^2} \omega\Delta^{-1}\omega\; \mu .\]and
\[E_2(\theta) = \frac{1}{2}\int_{S^2} \theta\Delta\theta\;\mu .\]The corresponding Zeitlin-MHD model is then given by
\[\dot W = \frac{1}{\hbar}[-P, W] {+\frac{1}{\hbar}[-B, \Theta]} {+\nu \Delta_N W}\] \[\dot \Theta = \frac{1}{\hbar}[-P, \Theta] \phantom{+ \frac{1}{\hbar}[M,\Theta] + \nu \Delta_N W}\]where \(\Delta_N P = W\) and \(B = \Delta_N \Theta\), for the Hoppe-Yau Laplacian \(\Delta_N\).
To run the simulation, let’s use random, smooth initial \(W_0\) and \(\Theta_0\) distributed the same, as shown below:
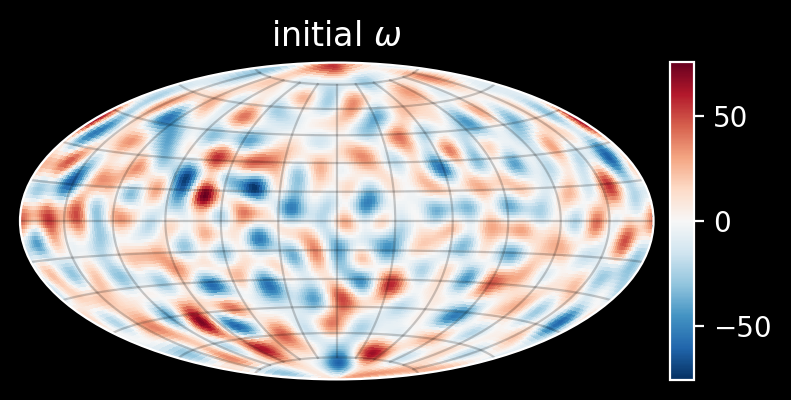
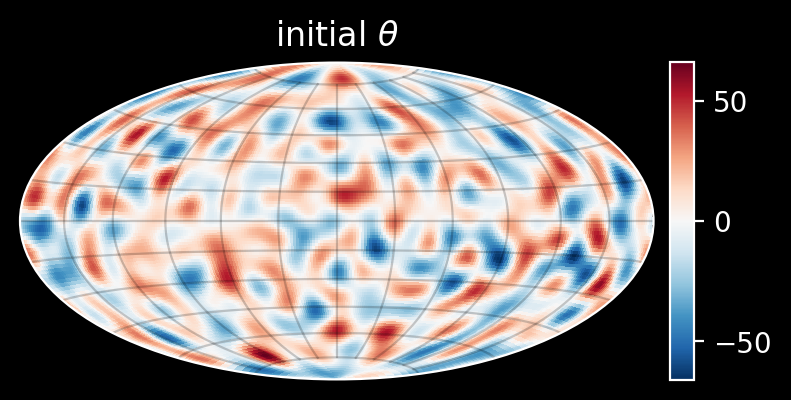
I run the simulation for long time with \(N=128\) for the viscosities \(\nu=1\), \(\nu = 0.1\), and \(\nu=0.01\). Whereas \(W\) converges to zero, the results indicate that the generic behavior for \(\Theta\) is to settle at two blobs, and that this point is reached faster for the smaller viscosity:
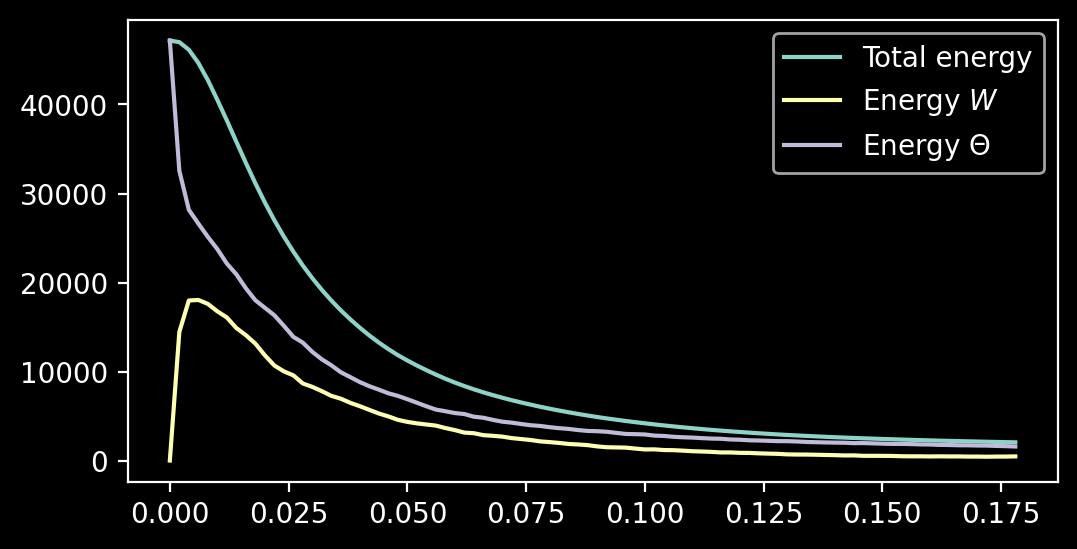
The total energy decreases in time, which follows from the calculation
\[\frac{d}{dt} H = -\mathrm{Tr}(\dot W P) - \mathrm{Tr}(\dot\Theta B) = \frac{1}{\hbar}\mathrm{Tr}(P([P, W] +[B, \Theta] -\nu \Delta_N W)) + \frac{1}{\hbar}\mathrm{Tr}(B[P,\Theta])\] \[= -\frac{\nu}{\hbar}\mathrm{Tr}(\Delta_N^{-1}W \Delta_N W) = - \frac{\nu}{\hbar} \lVert W \rVert_F^2 .\]But the partial energies \(E_1\) and \(E_2\) are not necessarily monotone. For the \(\nu=0.01\) simulation their evolution looks as follows: