Zeitlin model for beta-SQG
For \(\beta\in [0,1]\), an interpolation between 2-D Euler and SQG is given by
\[\dot\omega = \{\psi,\omega\}, \quad \Delta^{1-\beta/2}\psi = \omega \; .\]The corresponding Zeitlin model on \(\mathfrak{su}(N)\) is given by
\[\dot W = \frac{1}{\hbar} [P,W], \quad \Delta_N^{1-\beta/2} P = W \; .\]Here, we compute the inverse of the rational Laplacian via the spherical harmonic basis: if \(W = \sum_{\ell=0}^{N-1}\sum_{m=-\ell}^\ell\omega_{\ell m} T^N_{\ell m}\) then
\[P = \sum_{\ell=0}^{N-1}\sum_{m=-\ell}^\ell \frac{\omega_{\ell m}}{((\ell+1)\ell)^{1-\beta/2}} T^N_{\ell m} \; .\]I specify a random, but smooth initial \(W_0\) with \(\omega_{1 m} = 0\) (vanishing angular momentum). It looks as follows:
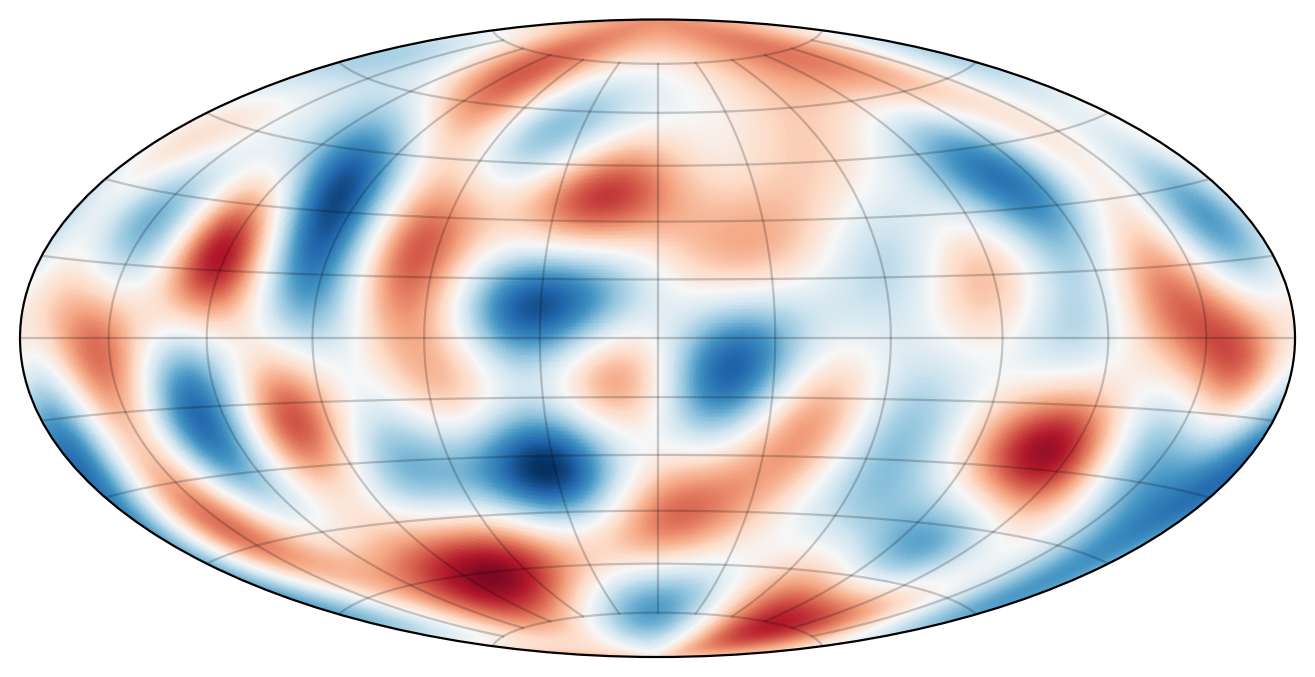
Physically, it’s kind of awkward to select the same initial vorticity for different choices of \(\beta\), as it implies that the initial velocities (or, equivalently, stream functions) are different. However, geometrically it makes sense, since all the simulations then evolve on the same co-adjoint orbit.
I run the simulation for long time with \(N=512\) for \(\beta = 0, 0.25, 0.5, 1.0\). The Euler case (\(\beta=0\)) yields the expected results: the formation of 4 interacting blobs. The other simulations show a similar asymptotic behavior: a final state of 4 interacting blobs.
Notice that the mixing phase is a little slower for larger \(\beta\), probably because the blobs are “sharper”. Theo Drivas hinted to me that this would be the case. I don’t have a good intuition for this mechanism yet, other than that we expect less regularity. Actually, the lower regularity is well reflected in the spectral energy plot:

Observations:
-
For all \(\beta\) we get a broken line corresponding to an inverse energy cascade.
-
The \(\beta=1\) is the limiting case when the slope is flat.
-
All slopes intersect in approximately the same point. This must correspond to the simulations evolving on the same co-adjoint orbit.